Cracking more passwords: qwerty-gen

Intro for über geeks:

This project was developed under the effects and hallucinations acquired throughout the search for the definition of complexity itself, most elegantly exposed by the acclaimed scientist Murray Gell-Mann in his book The Quark and the Jaguar: Adventures in the Simple and the Complex.

Anyone who is up to the task of cracking/finding passwords, wether it is by bruteforcing or dictionary attacks and against extracted hashes or vulnerable network/web app/embedded/large-etc-here services will most probably find himself stuck with complex (minus, mayus, numeric and special chars) passwords at one time or another.

In regard of the issue of the definiton of complexity, well, a book has already been referenced if someone didn't notice. For what's matter by now we'll use the already stated definition for password complexity, that is: it contains minuscules, majuscules, numbers and what is refered to as special characters.

It is farely easy for common users to generate passwords that comply with our definition of complexity even when such passwords have a really small amount of algorithmic information, very loosely that is: the length of the algorithm needed to reproduce a given sequence or password. It can be interpreted as the amount of randomness that exists between the chosen keys for a given password.

The latter statement will be proved by the simplicity of the following algorithms in the one-man battle for the correction and redefinition of the actual naive concept of complexity in authentication mechanisms used by computer systems.

Just as skape says in the excellent Safely Searching Process Virtual Address Space:'It is in this spirit that the author hopes to bring about a certain sense of safety for those who sometimes find it necessary to grope around haystacks in search of needles.'
 

Nuts and bolts:

One such set of passwords is the one made out of keyboard sequences. As complex sequences can be easily generated to bypass the usual 'the password does not meet the password policy requirements' one would reasonably believe there's a gigantic space of possibilities for the mad man guessing someone else's password, thus reducing his success rate.

In the hope of aiding such delirious man I bring to you qwerty-gen. Qwerty-gen is a set of simple algorithms designed for the generation of dictionaries and wordlists containing keyboard sequences for password cracking (or whatever other doomed use you find for it).

To achieve such task it will load a given keyboard layout into a simple python non-directed graph. A keyboard layout is composed of two files containing each key's symbol and it's according 'shift representation'. Of course this 'secondary representation' could be generalized but unless you're hacking some kind of submarine/space station/warp ship I doubt you'll ever use it.

Now, a few simple definitions are made to help in defining keyboard patterns:

This way the graph can be implemented in order to detect and preserve all the adjacent keys (neighbourhood) for every node in it. A DFS (Depth-First Search) algorithm was implemented according to these concepts in a way that limits pattern generations by depth. Yes, the A* algorithm could have been used here but we don't need anything that fancy as we will be running the search for all nodes in the graph taking into consideration this is a connected graph (for an arbitrarily large depth or password length) and nodes are marked as they are evaluated (so no repetitions).

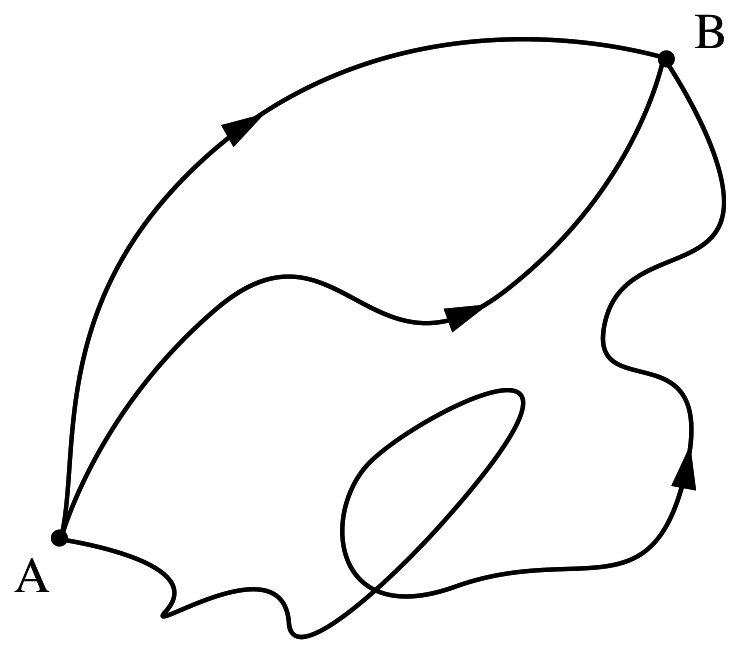
The search strategy for finding all paths of length n between keys X and Y is as follows:

• Create a simple list with all nodes in the graph
• Starting from the beginning find all paths of length n between index i and index j, such that:   n > j > i 
• Once j reaches n, increase i and set j to i+1
• Loop until i = n

 An intermediary step of this process would be as follows:

Where the gray area would already been calculated as opposed to the orange one. This guarantees all paths of length n are calculated from nodes [0,n) to nodes (0,n]. The invariant j > i won't allow for the finding of paths between say, A-Z; this is because the inverse path Z-A is actually A-Z. Just as it appears in many other situations:

Finally, we'll need a mechanism in which all shift permutations are generated for a given password. This so-called permutations are the cases in which one or more of the characters were swapped by pressing the shift key. So all permutations for password qwerty would be qwert, qwerT, qweRt, qweRT, qwErt, qwErT, qwERt, qwERT, qWert, qWerT, qWeRt, qWeRT, qWErt, qWErT, qWERt, qWERT, Qwert, QwerT, QweRt, QweRT, QwErt, QwErT, QwERt, QwERT, QWert, QWerT, QWeRt, QWeRT, QWErt, QWErT, QWERt and QWERT. Pretty neat example with 32 premutations or what?

If you have had any training in binary algebra/digital systems this will surely remember you the sequencing of binary digits. This makes up for a nice, simple algorithm for finding all shift permutations for a given password:

• Create a binary number starting at 1, pad it with 0s until it contains n bits
• Parse the whole number. If an active bit is found (1) swap the key at position i
• Increase counter
• Loop until counter = 2^n

In the end:

Although no practical algorithm can generate the vast space of keyboard sequences begotten by the human mind, qwerty-gen will generate every possible adjacent keyboard patterns. This leaves us with a very hopeless horizon in which common passwords like abc123 or q1w2e3r aren't generated (because abc and 123 as well as q1 and w2 are not adjacent patterns), but a few others like bvgftr54, zxdrfvb and even some eccentricities like °!"3ESZ, ZSw"!° and °!2WA<Z are, which have proven useful more than once in a while.

Don't you ph3ar though, because all in all we can still get better than this:



qwerty-gen source code can be found here: https://github.com/salcho/qwerty-gen 
keyseq_8chars_withperms.zip can be found IN GOOGLE DRIVE